Introdução
As loterias de números da Caixa são efetivadas por sorteio de bolas numeradas, colocadas em uma ou mais esferas, conforme figura baixo.

Nas loterias que vamos apresentar tem-se o número total de bolas e o número de bolas que serão sorteadas:
Quina: 80 bolas 5 sorteadas
Mega Sena: 60 bolas 6 sorteadas
Lotomania: 100 bolas 20 sorteadas
Dupla Sena: 50 bolas 6 sorteadas (2 vezes)
Lotofacil: 25 bolas 15 sorteadas
Federal: 10 bolas 5 sorteadas
A loteria Federal é diferente das anteriores pois são sorteados 5 bolas, de 5 esferas e 5 vezes, para gerar 5 números que podem variar de “00000” a “99999”, formando os 5 prêmios da extração. O número máximo possível varia ao longo do tempo da existência dessa loteria (desde 1962 sendo gerenciada pela Caixa) podendo ser, por exemplo, “39999”, “49999”, etc. Atualmente o número máximo é “99999”. Desta forma quando analisarmos essa loteria ao longo do tempo somente podemos considerar os últimos 4 números pois o primeiro pode estar limitado ao “3”, ou “4”, etc., conforme a época analisada.
Cálculos das probabilidades
Os cálculos das probabilidades das loterias são baseados em “combinações”, isto é, um número sorteado não pode participar novamente para a geração dos próximos números a serem sorteados. Se esse número voltar a participar do sorteio poderá haver repetição e o cálculo da probabilidade seria de outra forma (arranjos).
O cálculo de combinações de “n” bolas em grupos de “p” bolas é calculado usando “fatoriais” (multiplicações seqüenciais):
C(n,p) = n! / (p! * (n-p)!)
Para 4 bolas agrupadas 2 a 2 tem:
C(4,2)= 4! / (2! * 2!)
C(4,2)= (4*3*2*1) / (2*1*2*1)
C(4,2)=24 / 4 = 6
As 6 combinações são:
01 02
01 03
01 04
02 03
02 04
03 04
Para as três principais loterias em estudo tem-se:
Quina: C(80,5) = 80! / (5! * 75!)
C(80,5) = 80*79*78*77*76/5*4*3*2*1
C(80,5) = 2.884.801.920 / 120
C(80,5) = 24.040.016
C(80,5) = 24 milhões de combinações aproximadamente
Mega: C(60,6) = 60! / (6! * 54!)
C(60,6) = 60*59*58*57*56*55 / 6*5*4*3*2*1
C(60,6) = 36.045.979.200 /720
C(60,6) = 50.063.860
C(60,6) = 50 milhões de combinações aproximadamente
Lotofacil: C(25,15) = 25! / (15! * 10!)
C(25,15) = 3.268.760
C(25,15) = 3,3 milhões de combinações aproximadamente
Esses números são confirmados pelo site da Caixa, a saber:
Probabilidade da Quina:
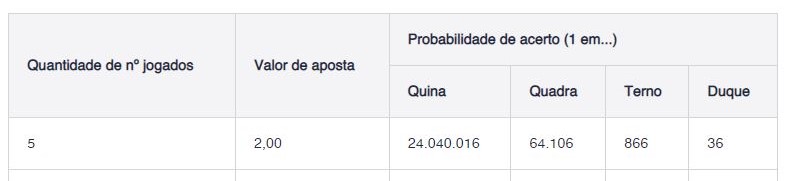
Probabilidade da Mega Sena:
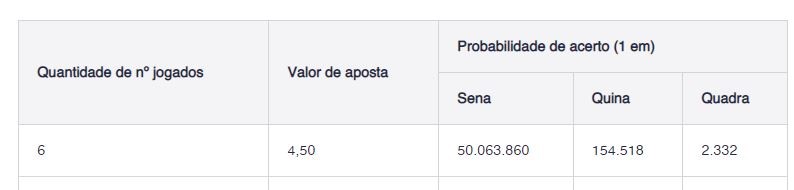
Probabilidade da Lotofacil:
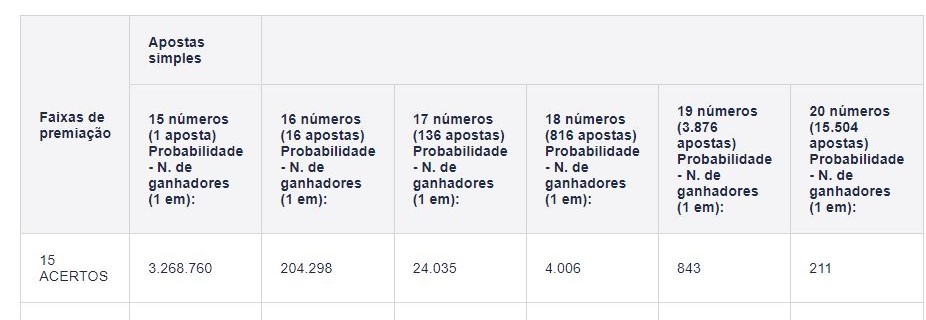
Esses valores, por serem muito elevados, são difíceis de serem avaliados (imaginados).
No caso da Mega Sena, loteria mais cobiçada e com os maiores prêmios, podemos ter uma idéia do que seriam 50 milhões de combinações de 6 números. Vamos começar pela primeira combinação de números, segunda, terceira e…. terminar com a última.
01 02 03 04 05 06
01 02 03 04 05 07
01 02 03 04 05 08
……
Combinações intermediárias…
……
53 54 55 56 57 58
54 55 56 57 58 59
55 56 57 58 59 60
A imagem que temos é um globo com as 60 bolas e a retirada de 6 bolas que formarão o resultado. Parece uma coisa simples, mas não é.
Vamos fazer uma nova “figuração” para as 50 milhões de combinações possíveis da Mega Sena. Seja, por exemplo, uma caixa de bilhetes de anotações da figura abaixo. Nessa caixa tem-se 300 bilhetes e ela tem uma espessura de 3 cm.

Se imaginarmos que TODAS as 50 milhões de combinações fossem escritas, uma em cada bilhete, teríamos o conjunto de combinações em forma de bilhetes de papel, ao invés das 60 bolas num globo. O sorteio seria escolher um bilhete qualquer, que contém uma das 50 milhões de combinações. Parece simples mas…
Quantas caixas de 300 bilhetes enfileiradas precisaríamos para tal operação?
300 bilhetes 1 caixa 3 cm
50.000.000 bilhetes 166.667 caixas 500.000 cm = 5.000 m = 5 km
Caminhando numa velocidade de 5,0 km/h teríamos de caminhar durante 1 hora para cobrir o trajeto das 166.667 caixas, uma encostada na outra, considerando o lado menor de 3 cm.
Esta é uma visão bastante real do que representam as combinações da Mega Sena. Ela dá uma idéia da complexidade do problema.
Para a Quina teríamos 24 milhões de combinações ou “andar” por 30 minutos.
Para a Lotofácil, com 3,3 milhões de combinações, 4 minutos.
Considerando as dimensões da caixa citada teríamos um volume total de 46 m3, equivalentes a uma sala com 4 m de comprimento, 4 m de largura e 2,9 m de altura, isto considerando os bilhetes empilhados como se ainda estivessem nas caixas, bem compactados!
Para obter esta postagem em Word baixe o arquivo indicado….